Shantibhushan Naik

Tag: story

  • Maintaining relationship – common friends

    I was posed a very trivial question from one of my friends recently. It picked my interest, since I could not readily solve it, and I had the inkling that there is a better, simple solution for this problem.

    The problem was, let’s say I have a table of users as below
    User's table data

    And these users have friends as below

    User's friends data or more easier to read as User's friends data

    Now, the trivial task was find common friends for users 1, and 5, hence naturally the answer should be

    User 1 : Woody’s friends, and User 5 : Andy’s friends  are

    Woody's friends and Andy's friends

    So, the question I had was what could be the best SQL query that would be return me this result?

    Woody and Andy's common friends

    I thought of 2 different SQL queries

    SELECT f.fid, u.name 'Woody and Andy\'s common friends' FROM
    (SELECT f.`fid` FROM friends f
    WHERE f.`uid` IN (1,5)
    GROUP BY f.`fid` HAVING COUNT(f.`fid`) > 1) f INNER JOIN user u ON (u.uid=f.fid)

    -or- another one was

    SELECT f.fid, u.name 'Woody and Andy\'s common friends' FROM
    (SELECT a.fid FROM
    (SELECT * FROM friends f
    WHERE f.`uid`=1) a INNER JOIN
    (SELECT * FROM friends f
    WHERE f.`uid`=5) b ON (a.fid=b.fid)) f INNER JOIN user u ON (u.uid=f.fid)

    Both seem to work, but is there any elegant way of getting common friends in a much simpler SQL query? At this moment, I logically find first SQL query more intuitive since all it does is pickup friends who appear more than once when users are 1 and 5. The second SQL query seems plain brute force approach.

  • Tired of teaching how to think

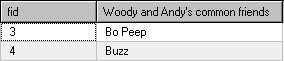
    Sir Ernest Rutherford, President of the Royal Academy, and recipient of the Nobel Prize in Physics, related the following story:

    “Some time ago I received a call from a colleague. He was about to give a student a zero for his answer to a physics question, while the student claimed a perfect score. The instructor and the student agreed to an impartial arbiter, and I was selected.

    I read the examination question: “Show how it is possible to determine the height of a tall building with the aid of a barometer.”

    The student had answered: “Take the barometer to the top of the building,attach a long rope to it, lower it to the street, and then bring it up, measuring the length of the rope. The length of the rope is the height of the building.”

    The student really had a strong case for full credit since he had really answered the question completely and correctly! On the other hand, if full credit were given, it could well contribute to a high grade in his physics course and certify competence in physics, but the answer did not confirm this. I suggested that the student have another try. I gave the student six minutes to answer the question with the warning that the answer should show some knowledge of physics.

    At the end of five minutes, he hadn’t written anything. I asked if he wished to give up, but he said he had many answers to this problem; he was just thinking of the best one. I excused myself for interrupting him and asked him to please go on. In the next minute, he dashed off his answer, which read: “Take the barometer to the top of the building and lean over the edge of the roof. Drop the barometer, timing its fall with a stopwatch.

    Then, using the formula x=0.5*a*t^2, calculate the height of the building.”

    At this point, I asked my colleague if he would give up. He conceded, and gave the student almost full credit. While leaving my colleague’s office, I recalled that the student had said that he had other answers to the problem, so I asked him what they were.

    “Well,” said the student, “there are many ways of getting the height of a tall building with the aid of a barometer. For example, you could take the barometer out on a sunny day and measure the height of the barometer, the length of its shadow, and the length of the shadow of the building, and by the use of simple proportion, determine the height of the building.”

    “Fine,” I said, “and others?”

    “Yes,” said the student, “there is a very basic measurement method you will like. In this method, you take the barometer and begin to walk up the stairs. As you climb the stairs, you mark off the length of the barometer along the wall. You then count the number of marks, and his will give you the height of the building in barometer units.”

    “A very direct method.”

    “Of course. If you want a more sophisticated method, you can tie the barometer to the end of a string, swing it as a pendulum, and determine the value of g [gravity] at the street level and at the top of the building.

    From the difference between the two values of g, the height of the building, in principle, can be calculated.”

    “On this same tack, you could take the barometer to the top of the building, attach a long rope to it, lower it to just above the street, and then swing it as a pendulum. You could then calculate the height of the building by the period of the precession”.

    “Finally,” he concluded, “probably the best,” he said, “is to take the barometer to the basement and knock on the superintendent’s door. When the superintendent answers, you speak to him as follows: ‘Mr. Superintendent, here is a fine barometer. If you will tell me the height of the building, I will give you this barometer.”

    At this point, I asked the student if he really did not know the conventional answer to this question. He admitted that he did, but said that he was fed up with high school and college instructors trying to teach him how to think.

    The name of the student was…

    Neils Bohr

    The Nobel Prize winner in Physics 1922